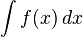Определение. Функция F (x) называется первообразной для функции f (x) на данном промежутке, если для любого х из данного промежутка F'(x)= f (x).

Основное свойство первообразных.

Если F (x) – первообразная функции f (x), то и функция F (x)+ C , где C –произвольная постоянная, также является первообразной функции f (x) (т.е. все первообразные функции f(x) записываются в виде F(x) + С ).

Геометрическая интерпретация.

Графики всех первообразных данной функции f (x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси Оу.

Таблица первообразных.

Правила нахождения первообразных .

Пусть F(x) и G(x) – первообразные соответственно функций f(x) и g(x). Тогда:

1. F ( x ) ± G ( x ) – первообразная для f ( x ) ± g ( x );

2. а F ( x ) – первообразная для а f ( x );

3. – первообразная для а f ( kx + b ).

Первообразная

[править]

Материал из Википедии — свободной энциклопедии

Текущая версия (не проверялась)

Перейти к: навигация, поиск

В математическом анализе первообра́зной (первоо́бразной) или примити́вной функцией данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Для примера: $F (x) = x 3 / 3$ является первообразной $f (x) = x 2$ . Так как производная константы равна нулю, $x 2$ будет иметь бесконечное количество первообразных; таких как $x 3 / 3 + 45645$ или $x 3 / 3 - 36$ … и т. д.; таким образом семейство первообразных функции $x 2$ можно обозначить как $F (x) = x 3 / 3 + C$ , где C — любое число. Графики таких первообразных смещены вертикально друг относительно друга, и их положение зависит от значения C.

Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

$\int\limits_a^b f(x)\, dx = F(b) - F(a).$

Это соотношение называется формулой Ньютона — Лейбница.

Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:

$\int f(x)\, dx$

Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.

Каждая непрерывная функция f имеет первообразную F, которая представляется в виде интеграла от f с переменным верхним пределом:

$F(x) = \int\limits_a^x f(t)\,dt.$

Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, 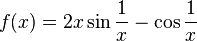$f(x) = 2x\sin\frac{1}{x}-\cos\frac{1}{x}$ с $f (0) = 0$ не непрерывна при $x = 0$ , но имеет первообразную $F(x) = x^2 sin\frac{1}{x}$ с $F (0) = 0$ .

Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:

$\int e^{-x^2}\,dx,\qquad \int \frac{\sin(x)}{x}\,dx,\qquad \int\frac{1}{\ln x}\,dx.$

Более развёрнутое изложение этих фактов можно отыскать в дифференциальной теории Галуа.

Содержание

[убрать]

[править] Свойства первообразной

Первообразная суммы равна сумме первообразных
Первообразная произведения константы и функции равна произведению константы и первообразной функции
Достаточным условием существования первообразной у заданной на отрезке функции $f$ является непрерывность $f$ на этом отрезке
Необходимыми условиями существования являются принадлежность функции $f$ первому классу Бэра и выполнение для неё свойства Дарбу
У заданной на отрезке функции любые две первообразные отличаются на постоянную.

[править] Техника интегрирования

Основная статья: Методы интегрирования

Нахождение первообразных значительно сложнее, чем нахождение производных. Для этого имеется несколько методов:

линейность интегрирования позволяет разбивать сложные интегралы на части,
интегрирование через подстановку, часто применяемое вместе с тригонометрическими тождествами или натуральным логарифмом,
интегрирование по частям для операций с произведениями функций,
метод обратной цепочки, особый случай интегрирования по частям,
метод интегрирования рациональных дробей позволяет интегрировать любые рациональные функции (дроби с полиномами в числителе и знаменателе),
алгоритм Риша (Risch algorithm),
некоторые интегралы можно найти в таблице интегралов,
при многократном интегрировании можно использовать дополнительную технику, для примера см. двойной интеграл и полярные координаты, Якобиан и теорема Стокса,
вычислительные пакеты помогают автоматизировать некоторые вышеприведённые символические операции, что очень удобно, когда алгебраические вычисления становятся слишком громоздкими,
если функция не имеет элементарной первообразной (как, например, $\exp\left(x^2\right)$ ), её интеграл может быть вычислен приближённо с помощью численного интегрирования.

[править] Другие определения

Это определение является наиболее распространенным, но встречаются и другие, в которых ослаблены требования существования всюду конечной $F'$ и выполнения всюду равенства $F'(x) = f (x)$ , иногда в определении используют обобщения производной.