Производные высших порядков

Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

$f^{(0)}(x_0) \equiv f(x_0).$

Если функция $f$ дифференцируема в $x 0$ , то производная первого порядка определяется соотношением

$f^{(1)}(x_0) \equiv f'(x_0).$

Пусть теперь производная $n$ -го порядка $f (n)$ определена в некоторой окрестности точки $x 0$ и дифференцируема. Тогда

$f^{(n+1)}(x_0) = \left(f^{(n)}\right)'(x_0).$

Производные высших порядков обозначаются символами:

$f^{(n)}(x_0) = \mathrm{D}^n\!f(x_0) = \frac{d^n\!f(x_0)}{dx^n}.$

Когда $n$ мало, используются штрихи, римские цифры или точки:

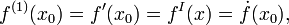
$f^{(1)}(x_0) = f'(x_0) = f^I(x) = \dot{f}(x_0),$; $f^{(2)}(x_0) = f''(x_0) = f^{II}(x) = \ddot{f}(x_0),$; $f (3) (x 0) = f'''(x 0) = f I I I (x),$ и т. д.
Производные высших порядков

  Ясно, что производная
функции y =f (x) есть также функция от x:

y' =f ' (x)
.
  Если функция f ' (x) дифференцируема, то её производная обозначается символом y'' =f '' (x) и называется второй производной функции f(x) или производной функции f(x) второго порядка. Пользуясь обозначением
можем написать

Пример.

  Очень удобно пользоваться также обозначением
, указывающим, что функция y=f(x) была продифференцирована по x два раза.
  Производная второй производной, т.е. функции y''=f '' (x) , называется третьей производной функции y=f(x) или производной функции f(x) третьего порядка и обозначается символами
.   Вообще n-я производная или производная n-го порядка функции y=f(x) обозначается символами

8. Производные высших порядков.

Пусть функция y = f(x) имеет производную f'(x) в каждой точке x некоторого множества D. Тогда ее производную f'(x) можно рассматривать как функцию, определенную на множестве D. В свою очередь функция f'(x) может в некоторых точках множества D иметь производную. В этом случае производной второго порядка (второй производной) называется производная от производной (f'(x))'. Для второй производной функции y = f (x) в точке x применяются обозначения:

Аналогично определяются производные 3-го, 4-го, и т.д. порядков. Производной первого порядка (или первой производной) считается f '(x).

Пример. y = sin 3x. Найти производные 1-го, 2-го, 3-го порядков и y⁽³⁾(p).

Решение. y' = 3 cos 3x, y'' = - 9sin 3x, y⁽³⁾ = - 27 cos 3x, y⁽³⁾(p) = - 27 cos 3p = 27.