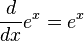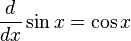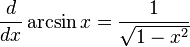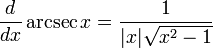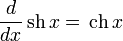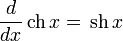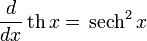Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференци́рованием.

Определение

Пусть в некоторой окрестности точки 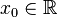x_0 \in \R определена функция 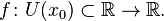f\colon U(x_0) \subset \R \to \R. Производной функции f в точке x0 называется предел, если он существует,

\lim\limits_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0}.

Общепринятые обозначения производной функции y = f(x) в точке x0:

f'(x_0) = f'_x(x_0)=\mathrm{D}\!f(x_0) = \frac{df(x_0)}{dx} = \left.\frac{dy}{dx}\right\vert_{x = x_0} = \dot{y}(x_0).

Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).

[править] Дифференцируемость

Основная статья: Дифференцируемая функция

Производная f'(x0) функции f в точке x0, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x0 тогда и только тогда, когда её производная в этой точке существует и конечна:

f \in \mathcal{D}(x_0)\Leftrightarrow\exists f'(x_0) \in (-\infty;\infty).

Для дифференцируемой в x0 функции f в окрестности U(x0) справедливо представление

f(x) = f(x0) + f'(x0)(x − x0) + o(x − x0) при x \to x_0.

Дифференциал функции.
Df - Дифференциал функции точки Xo, наз-ся главная линейная часть, приращения дифференциируемого функции. df(Xo) = A (дельта)Х <=> df (Xo) = f' (Xo) (дельта)X
 
Замечания. Для функции y=f(x) дифференциированной точке Х, дифференциал функции представили в виде6 dy=f'(x) по dx

Если z=z(x), то dz=z'(x)dz
Если y=2sin3x, то dy=6cos3xdx

Геометрический смысл дифференциированной функции


Дифференциал функции в точке, если приращения ординаты точки Мо, при перемещении точки Мо по касательной к графику функции y=f(x) в точке Мо с изменением Хо на (дельта)Х
Таблица производных

Правила дифференцирования общих функций

\left({cf}\right)' = cf'
\left({f + g}\right)' = f' + g'
\left({f - g}\right)' = f' - g'
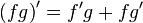\left({fg}\right)' = f'g + fg' (известно как «правило Лейбница»)
\left({f \over g}\right)' = {f'g - fg' \over g^2}, \qquad g \ne 0
(f^g)' = \left(e^{g\ln f}\right)' = f^g\left(f'{g \over f} + g'\ln f\right),\qquad f > 0
(f \circ g)' = (f' \circ g)g' — правило дифференцирования сложной функции
f' = (\ln f)'f, \qquad f > 0

[править] Производные простых функций

{d \over dx} c = 0
{d \over dx} x = 1
{d \over dx} cx = c
{d \over dx} |x| = {x \over |x|} = \sgn x,\qquad x \ne 0
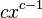{d \over dx} x^c = cx^{c-1},        когда x^c\,\! и cx^{c-1}\,\! определены
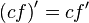
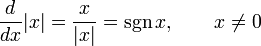
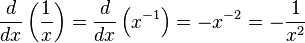
{d \over dx} \left({1 \over x}\right) = {d \over dx} \left(x^{-1}\right) = -x^{-2} = -{1 \over x^2}
{d \over dx} \left({1 \over x^c}\right) = {d \over dx} \left(x^{-c}\right) = -{c \over x^{c+1}}
{d \over dx} \sqrt{x} = {d \over dx} x^{1\over 2} = {1 \over 2} x^{-{1\over 2}} = {1 \over 2 \sqrt{x}}, \qquad x > 0
{d \over dx} \sqrt [n] {x} = {d \over dx} x^{1\over n} = {1 \over n} x^{-{n-1\over n}} = \frac {1} {n \cdot \sqrt [n] {x^{n-1}}}

[править] Производные экспоненциальных и логарифмических функций

{d \over dx} c^x = {c^x \ln c},\qquad c > 0
{d \over dx} e^x = e^x
{d \over dx} e^{f(x)} = f'(x)e^{f(x)}
{d \over dx} \log_c |x| = {1 \over x \ln c},\qquad c > 0, c \ne 1
{d \over dx} \ln x = {1 \over x}
{d \over dx} x^x = x^x(1+\ln x)

[править] Производные тригонометрических функций

{d \over dx} \sin x = \cos x
{d \over dx} \cos x = -\sin x
{d \over dx}\,\operatorname{tg}\,x = \sec^2 x = { 1 \over \cos^2 x}
{d \over dx}\,\operatorname{ctg}\,x = -\,\operatorname{cosec}^2\,x = { -1 \over \sin^2 x}
{d \over dx} \sec x =\,\operatorname{tg}\,x \sec x
{d \over dx} \,\operatorname{cosec}\,x = -\,\operatorname{ctg}\,x \,\operatorname{cosec}\,x
{d \over dx} \arcsin x = { 1 \over \sqrt{1 - x^2}}
{d \over dx} \arccos x = {-1 \over \sqrt{1 - x^2}}
{d \over dx} \,\operatorname{arctg}\,x = { 1 \over 1 + x^2}
{d \over dx} \arcsec x = { 1 \over |x|\sqrt{x^2 - 1}}
{d \over dx} \,\operatorname{arcctg}\,x = {-1 \over 1 + x^2}
{d \over dx} \,\operatorname{arccosec}\,x = {-1 \over |x|\sqrt{x^2 - 1}}

[править] Производные гиперболических функций

{d \over dx}\,\operatorname{sh}\,x = \,\operatorname{ch}\,x
{d \over dx}\,\operatorname{ch}\,x = \,\operatorname{sh}\,x
{d \over dx}\,\operatorname{th}\,x = \,\operatorname{sech}^2\,x
{d \over dx}\,\operatorname{sech}\,x = - \operatorname{th} x\,\operatorname{sech}\,x
{d \over dx}\,\operatorname{cth}\,x = -\,\operatorname{csch}^2\,x
{d \over dx}\,\operatorname{csch}\,x = -\,\operatorname{cth}\,x\,\operatorname{csch}\,x
{d \over dx}\,\operatorname{arsh}\,x = { 1 \over \sqrt{x^2 + 1}}
{d \over dx}\,\operatorname{arch}\,x = { 1 \over \sqrt{x^2 - 1}}
{d \over dx}\,\operatorname{arth}\,x = { 1 \over 1 - x^2}
{d \over dx}\,\operatorname{arsech}\,x = { 1 \over x\sqrt{1 - x^2}}
{d \over dx}\,\operatorname{arcth}\,x = { 1 \over 1 - x^2}
{d \over dx}\,\operatorname{arcsch}\,x = {-1 \over |x|\sqrt{1 + x^2}}

© 2008-2024
Админ