Первый замечательный предел
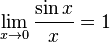
Доказательство
Рассмотрим односторонние пределы  и
и  и докажем, что они равны 1.
и докажем, что они равны 1.
Пусть  . Отложим этот угол на единичной окружности (R = 1).
. Отложим этот угол на единичной окружности (R = 1).
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.
Очевидно, что:
 (1)
(1)
(где SsectOKA — площадь сектора OKA)
(из 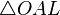 : | LA | = tgx)
: | LA | = tgx)
Подставляя в (1), получим:
Так как при  :
:
Умножаем на sinx:
Перейдём к пределу:
Найдём левый односторонний предел:
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
[править] Второй замечательный предел

Доказательство второго замечательного предела:
 Зная, что второй замечательный предел верен для натуральных значений x,
докажем второй замечательный предел для вещественных x, т.е. докажем,
что
Зная, что второй замечательный предел верен для натуральных значений x,
докажем второй замечательный предел для вещественных x, т.е. докажем,
что  . Рассмотрим два случая:
. Рассмотрим два случая:
1. Пусть  . Каждое значение x заключено между двумя положительными целыми числами:
. Каждое значение x заключено между двумя положительными целыми числами:  , где n = [x] - это целая часть x.
, где n = [x] - это целая часть x.
- Отсюда следует:
 , поэтому
, поэтому  .
.- Если
 , то
, то  . Поэтому, согласно пределу
. Поэтому, согласно пределу  , имеем:
, имеем: 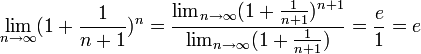
 .
.- По признаку (о пределе промежуточной функции) существования пределов
 .
.
2. Пусть  . Сделаем подстановку − x = t, тогда
. Сделаем подстановку − x = t, тогда
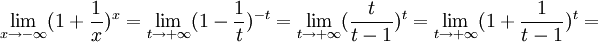
 .
.
Из двух этих случаев вытекает, что  для любого x.
для любого x. 
Следствия
Доказательство следствия
Следствия из второго замечательного предела:
[править] Замечательный логарифмический предел
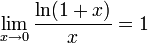
Доказательство предела
[править] Замечательный показательный предел

Следствия
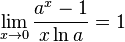 для
для  ,
, 
Доказательство предела
Доказательство следствия
[править] Замечательный степенной предел

Доказательство предела


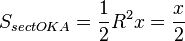







![\lim_{x \to 0-}\frac{\sin x}{x} =
\left [ \begin{matrix}
u = -x \\
x = -u \\
u \to 0+ \\
x \to 0-
\end{matrix} \right ] =
\lim_{u \to 0+}\frac{\sin(-u)}{-u} =
\lim_{u \to 0+}\frac{-\sin(u)}{-u} =
\lim_{u \to 0+}\frac{\sin(u)}{u} = 1](http://upload.wikimedia.org/math/4/c/5/4c5db8c436f5756f48fb3a8261329140.png)





![\lim_{x \to 0}\frac{\arcsin x}{x} =
\left [ \begin{matrix}
u = \arcsin x \\
x = \sin u \\
u \to 0 \\
x \to 0
\end{matrix} \right ] =
\lim_{u \to 0}\frac{u}{\sin u} = 1](http://upload.wikimedia.org/math/4/d/f/4df6d6629cb4d2bba2dc3c0007eddfe1.png)
![\lim_{x \to 0}\frac{\arctan x}{x} =
\left [ \begin{matrix}
u = \arctan x \\
x = \tan u \\
u \to 0 \\
x \to 0
\end{matrix} \right ] =
\lim_{u \to 0}\frac{u}{\tan u} = 1](http://upload.wikimedia.org/math/6/9/f/69f745f43c4eeeebb3f9084043fa53d3.png)
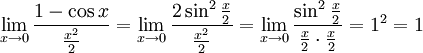


 , получим:
, получим:
 (1)
(1) убывет, поэтому величины
убывет, поэтому величины  возрастают. Поэтому последовательность
возрастают. Поэтому последовательность  — возрастающая, при этом
— возрастающая, при этом (2).
(2).
 .
. .
. (3).
(3). выполняются неравенства (2) и (3):
выполняются неравенства (2) и (3):  .
.
![\lim_{x \to \infty}(1 + \frac{k}{x})^x =
\left [ \begin{matrix}
u = \frac{k}{x} \\
x = \frac{k}{u} \\
u \to 0 \\
x \to \infty
\end{matrix} \right ] =
\lim_{u \to 0}(1 + u)^\frac{k}{u} =
(\lim_{u \to 0}(1 + u)^\frac{1}{u})^k =
e^k](http://upload.wikimedia.org/math/b/c/e/bce08dce054587008b869d0305b5794e.png)

![\lim_{x \to 0}\frac{e^x - 1}{x} =
\left [ \begin{matrix}
u = e^x - 1 \\
x = \ln(1 + u) \\
x \to 0 \\
u \to 0
\end{matrix} \right ] =
\lim_{u \to 0}\frac{u}{\ln(1 + u)} = 1](http://upload.wikimedia.org/math/7/f/1/7f1f77cf1f75ae01ab2d9806feddf01f.png)
![\lim_{x \to 0}\frac{a^x - 1}{x \ln a} =
\lim_{x \to 0}\frac{e^{\ln(a^x)} - 1}{x \ln a} =
\lim_{x \to 0}\frac{e^{x \ln a} - 1}{x \ln a} =
\left [ \begin{matrix}
u = x \ln a \\
u \to 0 \\
x \to 0
\end{matrix} \right ] =
\lim_{u \to 0}\frac{e^u - 1}{u} = 1](http://upload.wikimedia.org/math/e/0/3/e03c96d84ebe3bef9cfd46463c0ae2b7.png)
![\lim_{x \to 0}\frac{(1 + x)^\alpha - 1}{\alpha x} =
\lim_{x \to 0}\frac{e^{\alpha \ln(1+x)} - 1}{\alpha x} =
\left[ \ln(1+x) \sim x \right] =
\lim_{x \to 0}\frac{e^{\alpha x} - 1}{\alpha x} = 1](http://upload.wikimedia.org/math/4/5/5/455e0d87147f7b47d929137902ff52d4.png)
